Logistic Regression (رگرسیون لجستیک) در یادگیری ماشین چیست؟

Logistic Regression (رگرسیون لجستیک) در یادگیری ماشین چیست؟ راهنمای جامع

در دنیای هیجان‌انگیز یادگیری ماشین (Machine Learning)، الگوریتم‌های متعددی برای حل مسائل گوناگون توسعه یافته‌اند. یکی از این الگوریتم‌های بنیادین و بسیار پرکاربرد، Logistic Regression (رگرسیون لجستیک) است. برخلاف نامش که واژه “رگرسیون” را در خود دارد، رگرسیون لجستیک در حقیقت یک الگوریتم قدرتمند برای مسائل طبقه‌بندی (Classification) است و نه رگرسیون (پیش‌بینی مقادیر پیوسته).

این مقاله به طور جامع به این سوال پاسخ می‌دهد که Logistic Regression چیست، چگونه کار می‌کند، چه مزایا و معایبی دارد و چرا به عنوان یکی از اولین الگوریتم‌هایی که هر متخصص یادگیری ماشین باید آن را درک کند، شناخته می‌شود.

Logistic Regression چیست؟ تعریف و کاربرد

Logistic Regression یک الگوریتم طبقه‌بندی خطی است که برای پیش‌بینی احتمال وقوع یک رویداد دودویی (Binary Event) یا دسته‌بندی داده‌ها به دو دسته (یا بیشتر) استفاده می‌شود. به عبارت دیگر، این الگوریتم برای پاسخ به سوالاتی طراحی شده است که پاسخ آن‌ها “بله” یا “خیر” است.

مثال‌ها:
- آیا یک مشتری خاص، محصولی را خریداری خواهد کرد؟ (بله/خیر)
- آیا یک ایمیل خاص، هرزنامه (Spam) است یا عادی؟ (Spam/Not Spam)
- آیا یک بیمار، مبتلا به بیماری خاصی است یا خیر؟ (مبتلا/غیرمبتلا)

نقطه تمایز اصلی رگرسیون لجستیک با رگرسیون خطی (Linear Regression) این است که رگرسیون خطی یک مقدار پیوسته را پیش‌بینی می‌کند (مثلاً قیمت خانه)، در حالی که رگرسیون لجستیک یک احتمال بین 0 و 1 را پیش‌بینی می‌کند و سپس این احتمال را به یک کلاس (مثلاً 0 یا 1) تبدیل می‌کند.

←برای خرید کرک لایسنس تبلو Tableau با تمام ویژگی ها کلیک کنید

رگرسیون لجستیک چگونه کار می‌کند؟ تابع سیگموئید و مرز تصمیم

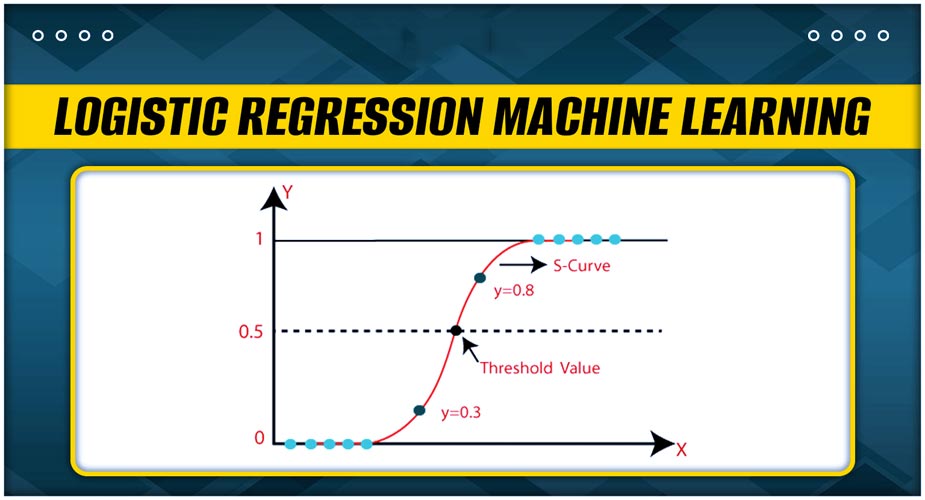
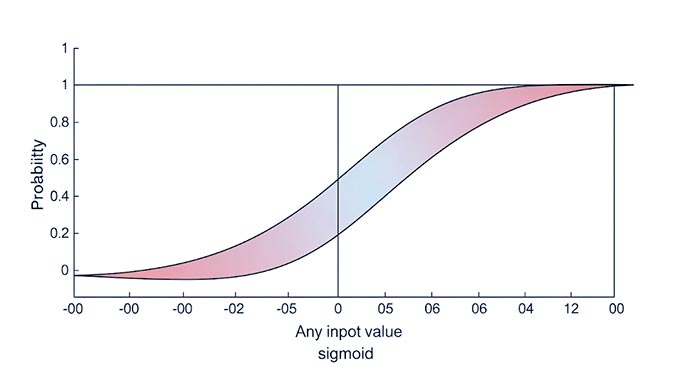
هسته اصلی Logistic Regression، تابع سیگموئید (Sigmoid Function) است که به آن تابع لجستیک (Logistic Function) نیز گفته می‌شود. این تابع دارای یک شکل “S” مانند است و هر مقدار ورودی را به یک مقدار خروجی بین 0 و 1 نگاشت می‌کند. این ویژگی، آن را برای تبدیل خروجی یک ترکیب خطی از ویژگی‌ها به یک احتمال مناسب می‌سازد.

فرمول تابع سیگموئید: $P (Y = 1∣ X) = σ (z) = 1 + e ^{- z} 1$

که در آن:

$P (Y = 1∣ X)$ احتمال تعلق نمونه به کلاس 1 (کلاس مثبت) است.
$σ$ (سیگما) نماد تابع سیگموئید است.
$e$ پایه لگاریتم طبیعی (اویلر) است.
$z$ یک ترکیب خطی از ویژگی‌های ورودی و ضرایب مدل (وزن‌ها) است، مشابه آنچه در رگرسیون خطی می‌بینیم: $z = b_{0} + b_{1} x_{1} + b_{2} x_{2} + \dots + b_{n} x_{n}$

مراحل کارکرد:

محاسبه ترکیب خطی ( $z$ ): ابتدا، رگرسیون لجستیک یک ترکیب خطی از ویژگی‌های ورودی (مانند سن، درآمد، سابقه خرید) و وزن‌های مربوط به آن‌ها را محاسبه می‌کند.
اعمال تابع سیگموئید: سپس، مقدار $z$ از طریق تابع سیگموئید عبور داده می‌شود. نتیجه این تابع، احتمالی بین 0 و 1 خواهد بود.
مرز تصمیم (Decision Boundary): برای تبدیل این احتمال به یک طبقه‌بندی نهایی (0 یا 1)، یک آستانه (Threshold) تعریف می‌شود. رایج‌ترین آستانه، 0.5 است.
- اگر احتمال پیش‌بینی شده $\geq 0.5$ باشد، نمونه به کلاس 1 (کلاس مثبت) تعلق می‌گیرد.
- اگر احتمال پیش‌بینی شده $< 0.5$ باشد، نمونه به کلاس 0 (کلاس منفی) تعلق می‌گیرد.

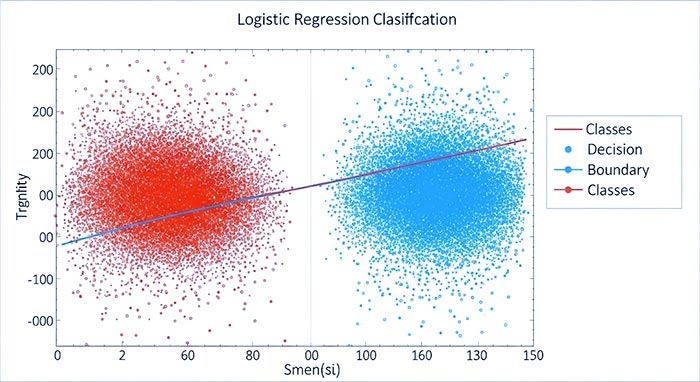
رگرسیون لجستیک یک مرز تصمیم خطی ایجاد می‌کند. به این معنی که اگر ویژگی‌ها را در یک فضای دوبعدی یا سه‌بعدی ترسیم کنیم، این مرز به صورت یک خط یا صفحه ظاهر می‌شود که دو کلاس را از هم جدا می‌کند.

تصویر 1: نمودار تابع سیگموئید (Logistic Function) که هر ورودی را به یک احتمال بین 0 و 1 نگاشت می‌کند.

آموزش مدل Logistic Regression: تابع هزینه و بهینه‌سازی

برای “آموزش” یک مدل Logistic Regression، هدف این است که بهترین مقادیر برای وزن‌ها (ضرایب $b_{0}, b_{1}, \dots b_{n}$ ) را پیدا کنیم که پیش‌بینی‌های مدل را تا حد امکان دقیق بسازند. این فرآیند از طریق بهینه‌سازی یک تابع هزینه (Cost Function) انجام می‌شود.

برخلاف رگرسیون خطی که از Mean Squared Error (MSE) استفاده می‌کند، رگرسیون لجستیک از Cross-Entropy Loss (که گاهی Log Loss نیز نامیده می‌شود) به عنوان تابع هزینه استفاده می‌کند. دلیل این امر این است که MSE برای احتمالات مناسب نیست و می‌تواند منجر به تابع هزینه‌ای غیرمحدب (Non-Convex) شود که الگوریتم‌های بهینه‌سازی را گیج می‌کند. Cross-Entropy Loss، یک تابع محدب (Convex) است که حداقل سراسری (Global Minimum) دارد و برای مسائل طبقه‌بندی احتمالاتی ایده‌آل است.

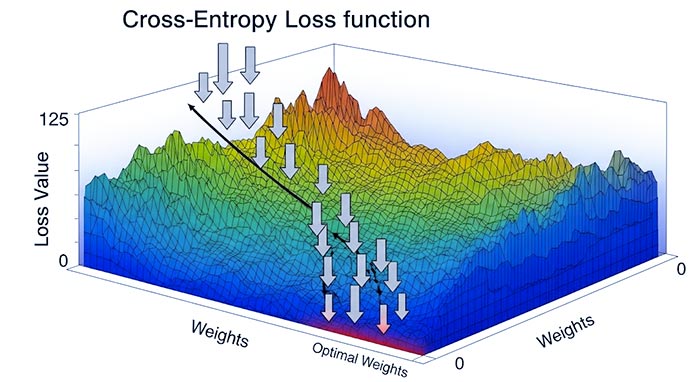
برای یافتن وزن‌های بهینه که تابع هزینه را حداقل می‌کنند، از الگوریتم‌های بهینه‌سازی مانند گرادیان نزولی (Gradient Descent) استفاده می‌شود. گرادیان نزولی به صورت تکراری وزن‌ها را در جهت مخالف گرادیان (شیب) تابع هزینه تنظیم می‌کند تا به نقطه حداقل برسد.

تصویر 2: یک نمودار دو بعدی از داده‌های طبقه‌بندی شده (دو کلاس با رنگ‌های متفاوت) که توسط یک مرز تصمیم خطی (که توسط رگرسیون لجستیک پیدا شده) از هم جدا شده‌اند.

مزایای Logistic Regression (مزایای رگرسیون لجستیک)

رگرسیون لجستیک به دلیل ویژگی‌های خاص خود، همچنان یک انتخاب محبوب در یادگیری ماشین است:

سادگی و قابلیت تفسیر: مدل نسبتاً ساده‌ای است و ضرایب آن به راحتی قابل تفسیر هستند (اثر هر ویژگی بر Log-Odds).
کارایی محاسباتی: از نظر محاسباتی بسیار کارآمد است و می‌تواند به سرعت روی مجموعه داده‌های بزرگ آموزش داده شود.
عملکرد خوب در مجموعه داده‌های کوچک: حتی با تعداد نسبتاً کمی از نمونه‌ها نیز می‌تواند عملکرد قابل قبولی داشته باشد.
ارائه احتمالات: به جای یک طبقه‌بندی بله/خیر صرف، یک احتمال را ارائه می‌دهد که می‌تواند برای سناریوهای مختلف تصمیم‌گیری (مانند تعیین آستانه‌های متفاوت) مفید باشد.
قابلیت تنظیم‌پذیری (Regularization): می‌تواند به راحتی با تکنیک‌های تنظیم‌پذیری (مانند L1 و L2) ترکیب شود تا از بیش‌برازش (Overfitting) جلوگیری کند.

معایب و محدودیت‌های رگرسیون لجستیک

با وجود مزایا، رگرسیون لجستیک محدودیت‌هایی نیز دارد:

فرض خطی بودن رابطه با Log-Odds: این مدل فرض می‌کند که بین ویژگی‌های ورودی و Log-Odds متغیر وابسته، یک رابطه خطی وجود دارد. اگر این فرض برقرار نباشد، عملکرد مدل کاهش می‌یابد.
حساسیت به داده‌های پرت (Outliers): مقادیر پرت می‌توانند به شدت بر وزن‌ها و در نتیجه بر عملکرد مدل تأثیر بگذارند.
ناتوانی در مدل‌سازی روابط پیچیده: برای مرزهای تصمیم‌گیری غیرخطی و پیچیده، رگرسیون لجستیک عملکرد ضعیف‌تری نسبت به الگوریتم‌های پیچیده‌تر (مانند شبکه‌های عصبی یا درختان تصمیم مبتنی بر Ensemble) دارد.
وابستگی به ویژگی‌های مستقل (Independent Features): فرض می‌کند که ویژگی‌های ورودی مستقل از یکدیگر هستند (عدم وجود Multicollinearity شدید).

تصویر 3: نموداری مفهومی از تابع هزینه (Cross-Entropy Loss) و فرآیند گرادیان نزولی که به سمت حداقل تابع حرکت می‌کند و وزن‌های بهینه را پیدا می‌کند.

Logistic Regression در مقابل Linear Regression

نام “رگرسیون لجستیک” گاهی اوقات می‌تواند گمراه‌کننده باشد، زیرا عملکرد آن بیشتر شبیه به یک طبقه‌بندی‌کننده است تا یک مدل رگرسیون. تفاوت اصلی بین این دو الگوریتم در خروجی آن‌ها و تابع پیوند (Link Function) است:

Linear Regression: یک مقدار پیوسته (نامحدود) را پیش‌بینی می‌کند و از تابع هویت به عنوان تابع پیوند استفاده می‌کند.
Logistic Regression: یک احتمال بین 0 و 1 را پیش‌بینی می‌کند و از تابع سیگموئید به عنوان تابع پیوند استفاده می‌کند تا خروجی را به این محدوده محدود کند.

کاربردهای Logistic Regression (کاربردهای رگرسیون لجستیک)

رگرسیون لجستیک به دلیل سادگی، تفسیرپذیری و کارایی خود، در صنایع مختلفی کاربرد فراوان دارد:

پیش‌بینی ریزش مشتری (Customer Churn Prediction): پیش‌بینی اینکه آیا مشتریان فعلی به استفاده از سرویس ادامه می‌دهند یا خیر.
امتیازدهی اعتباری (Credit Scoring): ارزیابی ریسک اعتباری متقاضیان وام.
تشخیص بیماری (Disease Diagnosis): پیش‌بینی حضور یا عدم حضور یک بیماری بر اساس علائم و نتایج آزمایش.
تشخیص هرزنامه (Spam Detection): طبقه‌بندی ایمیل‌ها به عنوان هرزنامه یا غیرهرزنامه.
پیش‌بینی پاسخ بازاریابی (Marketing Response Prediction): پیش‌بینی احتمال واکنش مشتری به یک کمپین تبلیغاتی.

نتیجه‌گیری

Logistic Regression (رگرسیون لجستیک) یک الگوریتم محوری در حوزه یادگیری ماشین است که با سادگی، قابلیت تفسیر و کارایی بالا، خود را به عنوان یک ابزار قدرتمند برای مسائل طبقه‌بندی دودویی (و چندکلاسه) اثبات کرده است. اگرچه ممکن است برای روابط غیرخطی بسیار پیچیده مناسب نباشد، اما توانایی آن در ارائه احتمالات و پایه و اساس قوی آن در آمار، آن را به گزینه‌ای عالی برای بسیاری از سناریوهای واقعی تبدیل می‌کند. درک رگرسیون لجستیک گام اولیه و ضروری برای هر کسی است که می‌خواهد به دنیای یادگیری ماشین وارد شود و بینش‌های عملیاتی را از داده‌ها استخراج کند.

مقاله های مرتبط:

1- بهترین کتابخانه های پایتون برای یادگیری ماشین

2- Rattle AI – داده کاوی و ابزار یادگیری ماشین

3- چگونه یادگیری ماشینی می تواند در داده کاوی مفید باشد

4-داشبورد سازی در نرم افزار تبلو و تجسم داده ها

download tableau desktop

امتیاز دهید

Logistic Regression (رگرسیون لجستیک) در یادگیری ماشین چیست؟