نحوه محاسبه میانگین متحرک نمایی (EMA) در پایتون

میانگین‌های متحرک (Moving Averages) شاخص‌های مالی هستند که برای تحلیل ارزش سهام در یک دوره زمانی طولانی استفاده می‌شوند، یعنی میانگین ارزش برای آن دوره طولانی محاسبه می‌شود.

میانگین متحرک نمایی (Exponential Moving Average – EMA) نوعی از میانگین‌های متحرک است. این شاخص به کاربران کمک می‌کند تا نویز را فیلتر کرده و یک منحنی هموار تولید کنند. در میانگین‌های متحرک، دو نوع بسیار محبوب هستند:

میانگین متحرک ساده (Simple Moving Average – SMA)
میانگین متحرک نمایی (Exponential Moving Average – EMA)

میانگین متحرک ساده فقط با انجام عملیات میانگین بر روی داده‌های داده شده، مقدار متوسط را محاسبه می‌کند، اما از بازه به بازه تغییر می‌کند. اما در میانگین متحرک نمایی، همچنین از میانگین ساده در محاسبه میانگین خود استفاده می‌شود، اما به مقادیر تازه اضافه شده وزن بیشتری داده می‌شود زیرا جدیدترین مقادیر دارای وزن بیشتری هستند.

←برای خرید کرک لایسنس تبلو Tableau با تمام ویژگی ها کلیک کنید

فرمول EMA:

$EM A_{T o d a y} = (Va l u e_{T o d a y} \times 1 + N o . O f D a ys C o n s t an t) + (EM A_{Y es t er d a y} \times (1 - 1 + N o . O f D a ys C o n s t an t))$

مقدار میانگین متحرک نمایی برای امروز با استفاده از مقدار قبلی میانگین متحرک نمایی محاسبه می‌شود.

در اینجا مقادیر قدیمی‌تر وزن کمتری و مقادیر جدیدتر وزن بیشتری پیدا می‌کنند. این کاهش وزن مقادیر با استفاده از یک مقدار ثابت به نام “Decay” محاسبه می‌شود. بنابراین با افزایش تعداد روزها، اهمیت مقدار کمتر می‌شود.

این کار به جلوگیری از نوسانات مقادیر کمک می‌کند.

استفاده از متد `ewm` در Pandas

متد میانگین وزنی نمایی (exponential Weighted Mean) برای محاسبه میانگین‌های متحرک استفاده می‌شود که یک ثابت “Decay” را به عنوان پارامتر می‌پذیرد.

ساختار (Syntax): DataFrameName.ewm(com=value).mean()

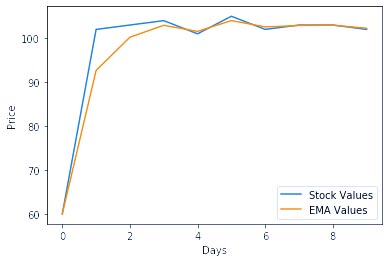
مثال 1: همانطور که در نمودار، خط EMA در مقایسه با مقادیر اصلی سهام کمی هموارتر شده است، این نشان‌دهنده ماهیت میانگین متحرک نمایی است.

Python

# import necessary packages
import pandas as pd
import matplotlib.pyplot as plt

# create a dataframe
stockValues = pd.DataFrame(
    {'Stock_Values': [10, 12, 11, 13, 15, 14, 16, 17, 15, 18, 19, 20, 18, 22, 23, 21, 24, 25, 23, 26, 27]}
)

# finding EMA
# use any constant value that results in
# good smoothened curve
ema = stockValues.ewm(com=0.4).mean()

# Comparison plot b/w stock values & EMA
plt.plot(stockValues, label="Stock Values")
plt.plot(ema, label="EMA Values")
plt.xlabel("Days")
plt.ylabel("Price")
plt.legend()
plt.show()

خروجی (Output):

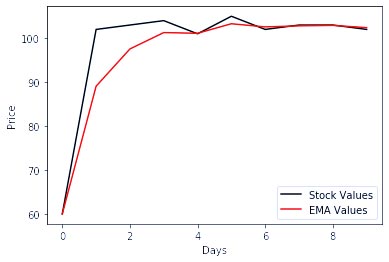
مثال 2: در کد زیر، از همان DataFrame که در بالا استفاده شد، با یک مقدار com متفاوت استفاده می‌کنیم که مقدار آن نسبت به مثال قبل بیشتر است. این مقدار به عنوان آرگومان به متد ewm پاس داده می‌شود.

Python

# import necessary packages
import pandas as pd
import matplotlib.pyplot as plt

# create a dataframe
stockValues = pd.DataFrame(
    {'Stock_Values': [10, 12, 11, 13, 15, 14, 16, 17, 15, 18, 19, 20, 18, 22, 23, 21, 24, 25, 23, 26, 27]}
)

# finding EMA
# used constant value as 0.8
ema = stockValues.ewm(com=0.8).mean()

# Comparison plot b/w stock values & EMA
plt.plot(stockValues, label="Stock Values", color="black")
plt.plot(ema, label="EMA Values", color="red")
plt.xlabel("Days")
plt.ylabel("Price")
plt.legend()
plt.show()

خروجی (Output):

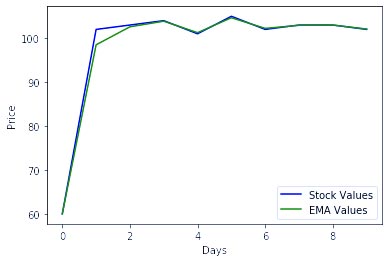
مثال 3: در اینجا همان DataFrame را که در 2 مثال بالا استفاده شد، با یک مقدار com متفاوت که تقریباً نزدیک به صفر است، به عنوان آرگومان به متد ewm پاس می‌دهیم.

Python

# import necessary packages
import pandas as pd
import matplotlib.pyplot as plt

# create a dataframe
stockValues = pd.DataFrame(
    {'Stock_Values': [10, 12, 11, 13, 15, 14, 16, 17, 15, 18, 19, 20, 18, 22, 23, 21, 24, 25, 23, 26, 27]}
)

# finding EMA
# com value=0.1 (0 approx)
ema = stockValues.ewm(com=0.1).mean()

# Comparison plot b/w stock values & EMA
plt.plot(stockValues, label="Stock Values", color="blue")
plt.plot(ema, label="EMA Values", color="green")
plt.xlabel("Days")
plt.ylabel("Price")
plt.legend()
plt.show()