خوشهبندی K-Means – مقدمه
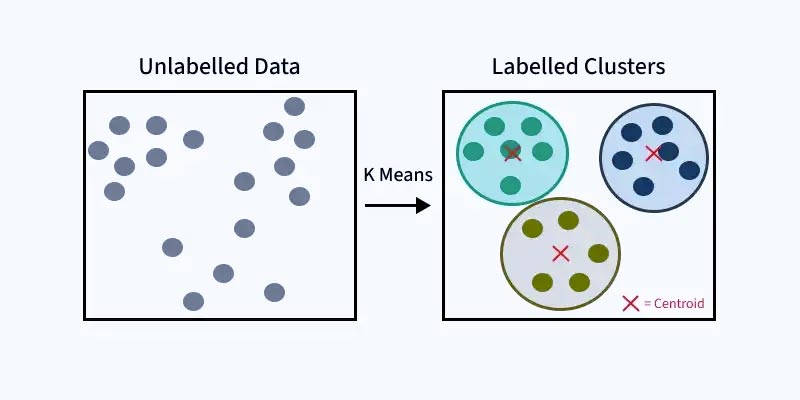
خوشهبندی K-Means یک الگوریتم یادگیری ماشین بدون نظارت (Unsupervised Machine Learning) است که مجموعه دادههای بدون برچسب را به خوشههای مختلف گروهبندی میکند. از این الگوریتم برای سازماندهی دادهها به گروههایی بر اساس شباهتشان استفاده میشود.
درک خوشهبندی K-Means:
برای مثال، یک فروشگاه آنلاین از K-Means برای گروهبندی مشتریان بر اساس فرکانس خرید و میزان خرج کردن استفاده میکند و بخشهایی مانند خریداران با بودجه کم، خریداران مکرر و خریداران بزرگ را برای بازاریابی شخصیسازی شده ایجاد میکند.
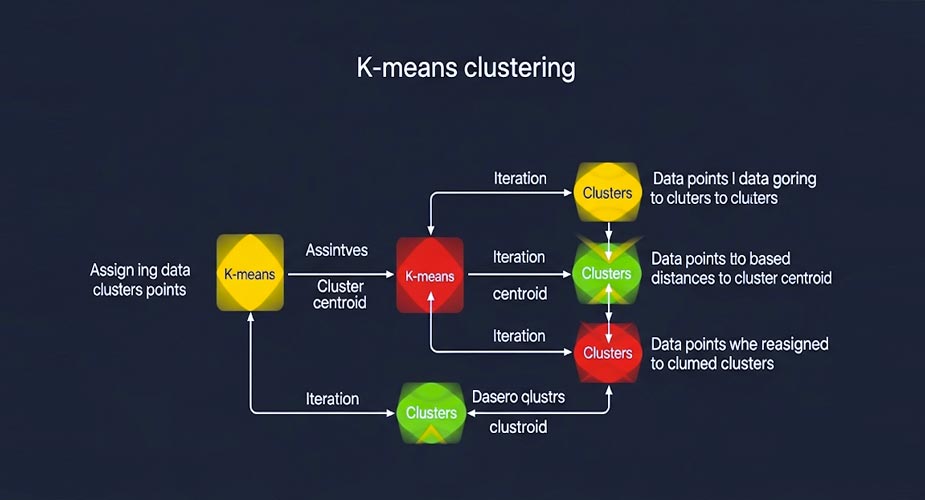
این الگوریتم ابتدا چند نقطه مرکزی به نام “سنتروید” (Centroids) را به صورت تصادفی انتخاب میکند. سپس هر نقطه داده به نزدیکترین سنتروید اختصاص داده میشود و یک خوشه را تشکیل میدهد. پس از اینکه تمام نقاط به یک خوشه اختصاص داده شدند، سنترویدها با یافتن میانگین موقعیت نقاط در هر خوشه بهروزرسانی میشوند. این فرآیند تا زمانی که سنترویدها از تغییر بازایستند و خوشهها شکل بگیرند، تکرار میشود.
هدف خوشهبندی، تقسیم نقاط داده به خوشههایی است که نقاط داده مشابه به یک گروه تعلق داشته باشند.
←برای خرید کرک لایسنس تبلو Tableau با تمام ویژگی ها کلیک کنید
خوشهبندی K-Means چگونه کار میکند؟
ما یک مجموعه داده از آیتمها را با ویژگیهای خاص و مقادیر برای این ویژگیها (مانند یک بردار) در اختیار داریم.
وظیفه این است که این آیتمها را به گروههایی دستهبندی کنیم. برای دستیابی به این هدف، از الگوریتم K-Means استفاده خواهیم کرد. ‘K’ در نام الگوریتم نشاندهنده تعداد گروهها/خوشههایی است که میخواهیم آیتمهایمان را در آنها طبقهبندی کنیم.
این الگوریتم آیتمها را به k گروه یا خوشه مشابه دستهبندی میکند. برای محاسبه این شباهت، از فاصله اقلیدسی به عنوان معیار اندازهگیری استفاده خواهیم کرد.
الگوریتم به شرح زیر کار میکند:
- ابتدا k نقطه را که “میانگین” (means) یا “سنترویدهای خوشه” (cluster centroids) نامیده میشوند، به صورت تصادفی مقداردهی اولیه میکنیم.
- هر آیتم را به نزدیکترین میانگین آن دستهبندی میکنیم.
- مختصات میانگینها را بهروزرسانی میکنیم، که میانگین مقادیر آیتمهای دستهبندی شده در آن خوشه تا به حال است.
- این فرآیند را برای تعداد مشخصی از تکرارها (iterations) تکرار میکنیم و در پایان، خوشههای خود را خواهیم داشت.
“نقاط” ذکر شده در بالا به این دلیل “میانگین” نامیده میشوند که مقادیر میانگین آیتمهای دستهبندی شده در آنها هستند.
برای مقداردهی اولیه این میانگینها، گزینههای زیادی وجود دارد. یک روش بصری این است که میانگینها را در آیتمهای تصادفی در مجموعه داده مقداردهی اولیه کنیم. روش دیگر این است که میانگینها را در مقادیر تصادفی بین مرزهای مجموعه داده مقداردهی اولیه کنیم. برای مثال، برای یک ویژگی x که آیتمها دارای مقادیر در [Min, Max] هستند، میانگینها را با مقادیر x در [Min, Max] مقداردهی اولیه خواهیم کرد.
انتخاب تعداد صحیح خوشهها برای تقسیمبندی معنیدار مهم است؛ برای انجام این کار، از روش آرنج (Elbow Method) برای یافتن مقدار بهینه k در K-Means استفاده میکنیم که یک ابزار گرافیکی برای تعیین تعداد بهینه خوشهها (k) در K-Means است.
پیادهسازی خوشهبندی K-Means در پایتون
ما از مجموعه داده make_blobs استفاده خواهیم کرد و نحوه ایجاد خوشهها را نشان خواهیم داد.
مرحله 1: وارد کردن کتابخانههای لازم ما Numpy، Matplotlib و scikit-learn را وارد میکنیم.
Python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
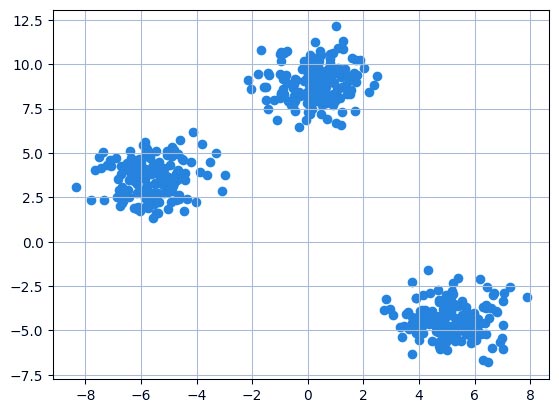
مرحله 2: ایجاد مجموعه داده سفارشی با make_blobs و رسم آن
Python
X, y = make_blobs(n_samples = 500, n_features = 2, centers = 3, random_state = 23)
fig = plt.figure(0)
plt.grid(True)
plt.scatter(X[:,0], X[:,1])
plt.show()
خروجی:
مرحله 3: مقداردهی اولیه سنترویدهای تصادفی این کد سه خوشه را برای خوشهبندی K-means مقداردهی اولیه میکند. یک seed تصادفی را تنظیم کرده و مراکز خوشه تصادفی را در یک محدوده مشخص تولید میکند و یک لیست خالی از نقاط برای هر خوشه ایجاد میکند.
Python
k = 3
clusters = {}
np.random.seed(23)
for idx in range(k):
# center = 2*(2*np.random.random((X.shape,))-1) # Original code had an error here for center shape
# The center should be 1D array, representing coordinates of one centroid
center = X[np.random.randint(X.shape[0]), :] # A common way: pick random points from X as initial centers
points = []
cluster = {
'center' : center,
'points' : []
}
clusters[idx] = cluster
# print(clusters) # Uncomment to see the initial clusters structure
خروجی:
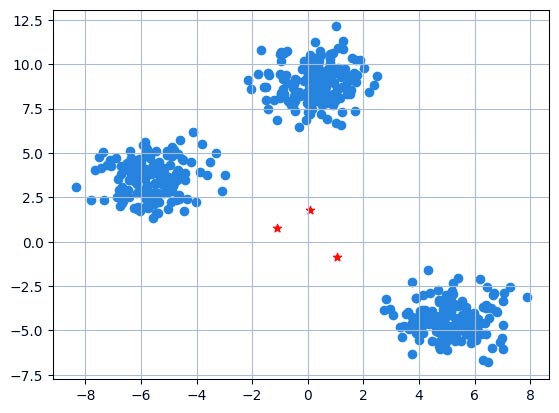
مرحله 4: رسم مرکز مقداردهی اولیه تصادفی با نقاط داده
Python
plt.scatter(X[:,0], X[:,1])
plt.grid(True)
for i in clusters:
center = clusters[i]['center']
plt.scatter(center[0], center[1], marker = '*', c = 'red', s=200) # s=200 for larger marker size
plt.show()
خروجی:
نمودار، یک نمودار پراکندگی از نقاط داده (X[:,0], X[:,1]) با خطوط شبکهای را نمایش میدهد. همچنین مراکز خوشه اولیه (ستارههای قرمز) که برای خوشهبندی K-means تولید شدهاند را علامتگذاری میکند.
مرحله 5: تعریف فاصله اقلیدسی
Python
def distance(p1,p2):
return np.sqrt(np.sum((p1-p2)**2))
مرحله 6: ایجاد تابع Assign و Update مرکز خوشه این مرحله، نقاط داده را به نزدیکترین مرکز خوشه اختصاص میدهد و مرحله M، مراکز خوشه را بر اساس میانگین نقاط اختصاص داده شده در خوشهبندی K-means بهروزرسانی میکند.
Python
def assign_clusters(X, clusters):
# Clear previous assignments
for i in range(len(clusters)):
clusters[i]['points'] = []
for idx in range(X.shape[0]): # Iterate over data points
dist = []
curr_x = X[idx]
for i in range(k):
dis = distance(curr_x, clusters[i]['center'])
dist.append(dis)
curr_cluster = np.argmin(dist)
clusters[curr_cluster]['points'].append(curr_x)
return clusters
def update_clusters(clusters): # X is not needed here
for i in range(k):
points = np.array(clusters[i]['points'])
if points.shape[0] > 0: # Check if points list is not empty
new_center = points.mean(axis = 0)
clusters[i]['center'] = new_center
# clusters[i]['points'] = [] # Points are cleared in assign_clusters
return clusters
مرحله 7: ایجاد تابع برای پیشبینی خوشه برای نقاط داده
Python
def pred_cluster(X, clusters):
pred = []
for i in range(X.shape[0]):
dist = []
for j in range(k):
dist.append(distance(X[i],clusters[j]['center']))
pred.append(np.argmin(dist))
return pred
مرحله 8: اختصاص، بهروزرسانی و پیشبینی مرکز خوشه
Python
# Run K-means algorithm for a few iterations
for _ in range(10): # Example: 10 iterations
clusters = assign_clusters(X, clusters)
clusters = update_clusters(clusters)
pred = pred_cluster(X, clusters)
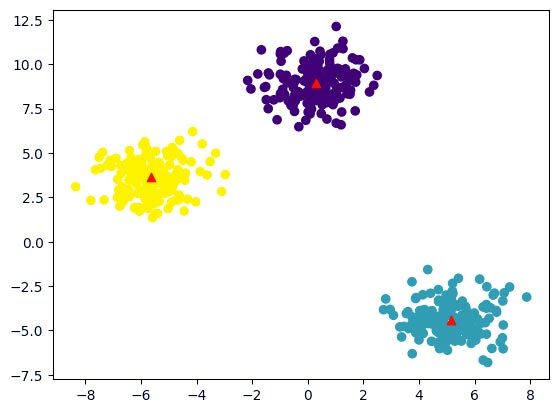
مرحله 9: رسم نقاط داده با مرکز خوشه پیشبینی شده آنها
Python
plt.scatter(X[:,0], X[:,1], c = pred)
for i in clusters:
center = clusters[i]['center']
plt.scatter(center[0], center[1], marker = '^', c = 'red', s=200) # s=200 for larger marker size
plt.show()
خروجی:
نمودار، نقاط داده را که با خوشههای پیشبینی شدهشان رنگآمیزی شدهاند، نشان میدهد. نشانگرهای قرمز، مراکز خوشه بهروزرسانی شده پس از مراحل E-M در الگوریتم خوشهبندی K-means را نشان میدهند.
مقاله های مرتبط:
1- نحوه محاسبه میانگین متحرک نمایی (EMA) در پایتون
2- مدل ARIMA برای پیش بینی سری های زمانی در پایتون
3- نحوه اجرای رگرسیون چند جمله ای در پایتون
4-داشبورد سازی در نرم افزار تبلو و تجسم داده ها