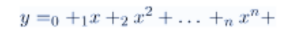نحوه اجرای رگرسیون چند جمله ای در پایتون

رگرسیون چند جمله ای شکلی از رگرسیون خطی است که در آن رابطه بین متغیر مستقل x و متغیر وابسته y به عنوان چند جمله ای درجه n مدل می شود. رگرسیون چند جمله ای با یک رابطه غیرخطی بین مقدار x و میانگین شرطی مربوط به y که E(y | x) نشان داده می شود، برازش می کند. در این مقاله به طور عمیق به رگرسیون چند جمله ای خواهیم پرداخت.

رگرسیون چند جمله ای چیست؟

برخی از روابط وجود دارد که یک محقق فرض می کند منحنی است. بدیهی است که چنین مواردی شامل یک اصطلاح چند جمله ای می شود.
بازرسی از باقیمانده ها. اگر بخواهیم یک مدل خطی را با داده‌های منحنی منطبق کنیم، یک نمودار پراکنده از باقیمانده‌ها (محور Y) روی پیش‌بینی‌کننده (محور X) دارای تکه‌هایی با بسیاری از باقیمانده‌های مثبت در وسط خواهد بود. از این رو در چنین شرایطی مناسب نیست.
یک فرض در تحلیل رگرسیون خطی چندگانه معمول این است که همه متغیرهای مستقل مستقل هستند. در مدل رگرسیون چند جمله ای، این فرض برآورده نمی شود.

←برای خرید کرک لایسنس تبلو Tableau با تمام ویژگی ها کلیک کنید

چرا رگرسیون چند جمله ای؟

رگرسیون چند جمله‌ای نوعی تحلیل رگرسیونی است که در آمار و یادگیری ماشینی استفاده می‌شود که رابطه بین متغیر مستقل (ورودی) و متغیر وابسته (خروجی) خطی نباشد. در حالی که رگرسیون خطی ساده رابطه را به عنوان یک خط مستقیم مدل می کند، رگرسیون چند جمله ای با برازش یک معادله چند جمله ای به داده ها، انعطاف پذیری بیشتری را امکان پذیر می کند.

زمانی که رابطه بین متغیرها با یک منحنی به جای یک خط مستقیم بهتر نشان داده شود، رگرسیون چند جمله ای می تواند الگوهای غیر خطی در داده ها را به تصویر بکشد.

رگرسیون چند جمله ای چگونه کار می کند؟

اگر به دقت مشاهده کنیم، متوجه خواهیم شد که از رگرسیون خطی به رگرسیون چند جمله ای تبدیل می شود. فقط قرار است شرایط مرتبه بالاتر ویژگی های وابسته را در فضای ویژگی اضافه کنیم. این گاهی اوقات به عنوان مهندسی ویژگی نیز شناخته می شود اما دقیقاً نیست.

هنگامی که رابطه غیر خطی است، یک مدل رگرسیون چند جمله ای، اصطلاحات چند جمله ای درجه بالاتر را معرفی می کند.

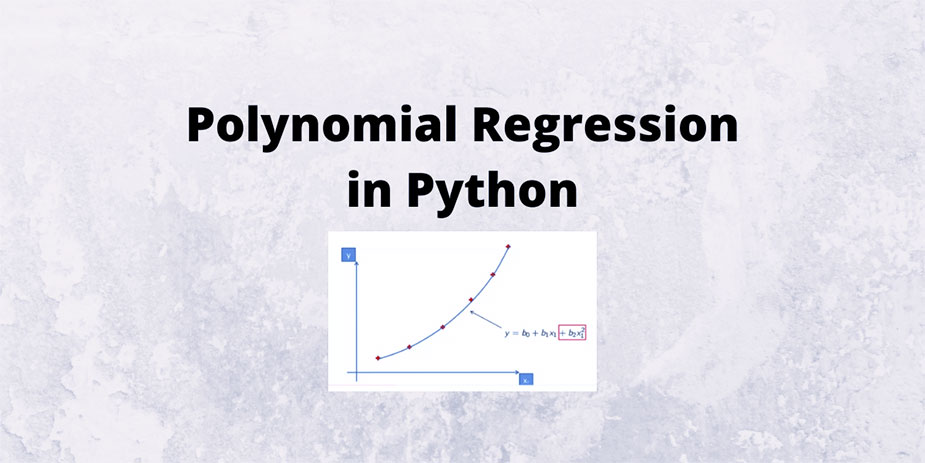
شکل کلی معادله رگرسیون چند جمله ای درجه n به صورت زیر است:

y متغیر وابسته است.
x متغیر مستقل است.
n,……..,1,0 ضرایب چند جمله ای هستند.
n درجه چند جمله ای است.
ϵ بیانگر عبارت خطا است.

هدف اصلی تحلیل رگرسیون مدل سازی مقدار مورد انتظار متغیر وابسته y بر حسب مقدار متغیر مستقل x است. در رگرسیون خطی ساده از معادله زیر استفاده کردیم:

y = a + bx + e

در اینجا y یک متغیر وابسته، a نقطه ی y، b شیب و e میزان خطا است. در بسیاری از موارد، این مدل خطی جواب نمی‌دهد، برای مثال، اگر تولید سنتز شیمیایی را بر حسب دمایی که سنتز در آن انجام می‌شود تحلیل کنیم، در چنین مواردی از یک مدل درجه دوم استفاده می‌کنیم.

y متغیر وابسته x است
a y- intercept و e نرخ خطا است.

به طور کلی، می توانیم آن را برای مقدار nام مدل کنیم.

از آنجایی که تابع رگرسیون از نظر متغیرهای مجهول خطی است، بنابراین این مدل ها از نقطه تخمین خطی هستند. بنابراین از طریق تکنیک حداقل مربع، مقدار پاسخ (y) را می توان محاسبه کرد.

با گنجاندن اصطلاحات درجه بالاتر (مکعبی، مکعبی و غیره)، مدل می‌تواند الگوهای غیرخطی در داده‌ها را ثبت کند.

انتخاب درجه چند جمله ای (n) یک جنبه حیاتی از رگرسیون چند جمله ای است. درجه بالاتر به مدل اجازه می دهد تا با داده های آموزشی بیشتر مطابقت داشته باشد، اما ممکن است منجر به بیش از حد برازش شود، به خصوص اگر درجه بسیار بالا باشد. بنابراین، درجه باید بر اساس پیچیدگی رابطه اساسی در داده ها انتخاب شود.
مدل رگرسیون چند جمله ای برای یافتن ضرایبی که تفاوت بین مقادیر پیش بینی شده و مقادیر واقعی در داده های آموزشی را به حداقل می رساند آموزش داده شده است.
هنگامی که مدل آموزش داده شد، می توان از آن برای پیش بینی داده های جدید و نادیده استفاده کرد. معادله چند جمله ای الگوهای غیر خطی مشاهده شده در داده های آموزشی را به تصویر می کشد و به مدل اجازه می دهد تا به روابط غیر خطی تعمیم یابد.

رگرسیون چند جمله ای مثال زندگی واقعی

بیایید یک مثال واقعی را برای نشان دادن کاربرد رگرسیون چند جمله ای در نظر بگیریم. فرض کنید شما در زمینه امور مالی مشغول به کار هستید و در حال تجزیه و تحلیل رابطه بین سالها تجربه (بر حسب سال) یک کارمند و حقوق مربوط به آن (به دلار) هستید. شما مشکوک هستید که این رابطه ممکن است خطی نباشد و درجات بالاتر چند جمله ای ممکن است پیشرفت حقوق را در طول زمان بهتر نشان دهد.

سابقه Years of Experience	حقوق (به دلار) Salary
1	50,000
2	55,000
3	65,000
4	80,000
5	110,000
6	150,000
7	200,000

حال، بیایید رگرسیون چند جمله‌ای را برای مدل‌سازی رابطه بین سال‌های تجربه و حقوق اعمال کنیم. برای این مثال از یک چند جمله ای درجه دوم (درجه 2) استفاده می کنیم.

معادله رگرسیون چند جمله ای درجه دوم:

Salary= $β_0+β_1$ ×Experience+ $β_2$ ×Experience^2+

اکنون، برای یافتن ضرایبی که تفاوت بین حقوق پیش‌بینی‌شده و حقوق واقعی را در مجموعه داده به حداقل می‌رسانند، می‌توانیم از روش حداقل مربعات استفاده کنیم. هدف به حداقل رساندن مجموع مجذور اختلاف بین مقادیر پیش بینی شده و مقادیر واقعی است.

پیاده سازی رگرسیون چند جمله ای با استفاده از پایتون

برای دریافت مجموعه داده مورد استفاده برای تجزیه و تحلیل رگرسیون چند جمله ای، اینجا را کلیک کنید. کتابخانه های مهم و مجموعه داده ای را که برای انجام رگرسیون چند جمله ای استفاده می کنیم، وارد کنید.

کتابخانه های پایتون مدیریت داده ها و انجام کارهای معمولی و پیچیده را با یک خط کد برای ما بسیار آسان می کند.

Pandas – این کتابخانه به بارگذاری قاب داده در قالب آرایه دو بعدی کمک می کند و دارای چندین عملکرد برای انجام وظایف تجزیه و تحلیل در یک حرکت است.
Numpy – آرایه های Numpy بسیار سریع هستند و می توانند محاسبات بزرگ را در زمان بسیار کوتاهی انجام دهند.
Matplotlib/Seaborn – از این کتابخانه برای ترسیم تصاویر استفاده می شود.
Sklearn – این ماژول شامل چندین کتابخانه با عملکردهای از پیش پیاده سازی شده برای انجام وظایف از پیش پردازش داده تا توسعه و ارزیابی مدل است.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
datas = pd.read_csv('data.csv')
datas

خروجی:

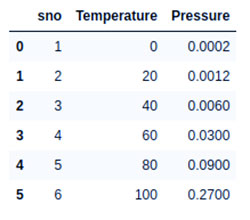
پنج ردیف اول مجموعه داده

متغیر ویژگی ما که X است شامل ستون بین 1 و متغیر هدف که y است شامل ستون دوم خواهد بود.

X = datas.iloc[:, 1:2].values
y = datas.iloc[:, 2].values

اکنون بیایید یک مدل رگرسیون خطی را بر روی داده‌های موجود برازش دهیم.

# Features and the target variables

X = datas.iloc[:, 1:2].values

y = datas.iloc[:, 2].values

# Fitting Linear Regression to the dataset

from sklearn.linear_model import LinearRegression

lin = LinearRegression()

lin.fit(X, y)

اکنون بیایید یک مدل رگرسیون خطی را بر روی داده‌های موجود برازش دهیم.

# Fitting Polynomial Regression to the dataset
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=4)
X_poly = poly.fit_transform(X)
poly.fit(X_poly, y)
lin2 = LinearRegression()
lin2.fit(X_poly, y)

در این مرحله، ما نتایج رگرسیون خطی را با استفاده از نمودار پراکندگی تجسم می‌کنیم.

# Visualising the Linear Regression results
plt.scatter(X, y, color='blue')
plt.plot(X, lin.predict(X), color='red')
plt.title('Linear Regression')
plt.xlabel('Temperature')
plt.ylabel('Pressure')
plt.show()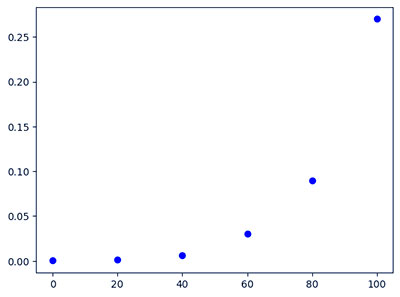

خروجی:

نمودار پراکندگی ویژگی و متغیر هدف

نتایج رگرسیون چند جمله ای را با استفاده از نمودار پراکندگی تجسم کنید.

# Visualising the Polynomial Regression results
plt.scatter(X, y, color='blue')
plt.plot(X, lin2.predict(poly.fit_transform(X)),
color='red')
plt.title('Polynomial Regression')
plt.xlabel('Temperature')
plt.ylabel('Pressure')
plt.show()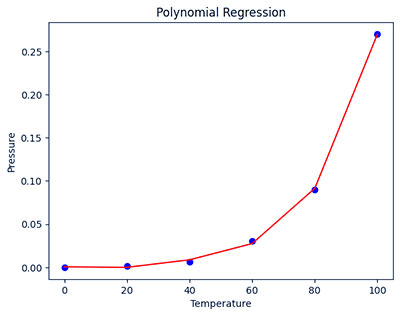

خروجی:

اجرای رگرسیون چند جمله ای

نتایج جدید را با رگرسیون خطی و چند جمله ای پیش بینی کنید. توجه داشته باشید که متغیر ورودی باید در یک آرایه Numpy 2D باشد.

# Predicting a new result with Linear Regression
# after converting predict variable to 2D array
pred = 110.0
predarray = np.array([[pred]])
lin.predict(predarray)

خروجی:

array([0.20675333])

# Predicting a new result with Polynomial Regression
# after converting predict variable to 2D array
pred2 = 110.0
pred2array = np.array([[pred2]])
lin2.predict(poly.fit_transform(pred2array))

خروجی:

array([0.43295877])

Overfitting در مقابل Under-Fitting

در حالی که با رگرسیون چند جمله‌ای سروکار داریم، مشکل بیش از حد برازش است، زیرا در حالی که ترتیب رگرسیون چند جمله‌ای را برای دستیابی به عملکرد بهتر و بهتر افزایش می‌دهیم، بر روی داده‌ها اضافه می‌شود و در نقاط داده جدید عمل نمی‌کند.

به همین دلیل تنها در حین استفاده از رگرسیون چند جمله ای، سعی می کنیم وزن های مدل را جریمه کنیم تا اثر مشکل اضافه برازش را منظم کنیم. تکنیک‌های منظم‌سازی مانند رگرسیون کمند و متدولوژی‌های رگرسیون ریج هر زمان که با موقعیتی سروکار داریم که در آن مدل ممکن است بیش از حد با داده‌های موجود مطابقت داشته باشد، استفاده می‌شود.

Bias در مقابل واریانس معامله

این تکنیک تعمیم رویکردی است که برای جلوگیری از مشکل بیش‌برازش و عدم تناسب استفاده می‌شود. در اینجا نیز این تکنیک به ما کمک می‌کند تا با انتخاب مقدار مناسب برای درجه چندجمله‌ای که می‌خواهیم داده‌های خود را بر آن تطبیق دهیم، از مشکل بیش از حد برازش اجتناب کنیم. به عنوان مثال، این زمانی به دست می آید که پس از افزایش درجه چند جمله ای پس از یک سطح مشخص، شکاف بین معیارهای آموزشی و اعتبارسنجی شروع به افزایش می کند.

کاربرد رگرسیون چند جمله ای

دلیل استفاده گسترده از رگرسیون چند جمله‌ای این است که تقریباً تمام داده‌های دنیای واقعی ماهیت غیرخطی دارند و از این رو وقتی یک مدل غیرخطی را روی داده‌ها یا یک خط رگرسیون منحنی قرار می‌دهیم، نتایجی را که بدست آوردن به مراتب بهتر از آنچه می توانیم با رگرسیون خطی استاندارد به دست آوریم هستند. برخی از موارد استفاده از رگرسیون چند جمله ای به شرح زیر است:

سرعت رشد بافت ها
پیشرفت اپیدمی های بیماری
توزیع ایزوتوپ های کربن در رسوبات دریاچه

مزایا و معایب استفاده از رگرسیون چند جمله ای

مزایای استفاده از رگرسیون چند جمله ای

طیف وسیعی از عملکردها را می توان در زیر آن قرار داد.
چند جمله ای اساساً با طیف گسترده ای از انحناها مطابقت دارد.
چند جمله ای بهترین تقریب از رابطه بین متغیرهای وابسته و مستقل را ارائه می دهد.

معایب استفاده از رگرسیون چند جمله ای

اینها نسبت به موارد پرت بسیار حساس هستند.
وجود یک یا دو نقطه پرت در داده ها می تواند نتایج تحلیل غیرخطی را به طور جدی تحت تاثیر قرار دهد.
علاوه بر این، متاسفانه ابزارهای اعتبارسنجی مدل کمتری برای تشخیص نقاط پرت در رگرسیون غیرخطی نسبت به رگرسیون خطی وجود دارد.

نتیجه گیری

رگرسیون چند جمله ای، یک ابزار همه کاره، کاربردهایی را در حوزه های مختلف پیدا می کند. در حالی که به روابط غیر خطی پرداخته می شود، نیاز به بررسی دقیق بیش از حد برازش و پیچیدگی مدل دارد.

مقاله های مرتبط:

1- چگونه یادگیری ماشینی می تواند در داده کاوی مفید باشد

2- آستانه داده GA4 چیست؟

3- کدام پایگاه داده برای یادگیری ماشینی بهتر است؟

4-داشبورد سازی در نرم افزار تبلو و تجسم داده ها

download tableau desktop

امتیاز دهید

نحوه اجرای رگرسیون چند جمله ای در پایتون